Simetri Lipat dan Putar Pada Bangun Datar Beserta Contohnya – Bangun datar adalah bangun dua demensi yang hanya memiliki panjang dan lebar, yang dibatasi oleh garis lurus atau lengkung. Jenis bangun datar bermacam-macam, antara lain persegi, persegi panjang, segitiga, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran. Pada setiap bangun datar terdapat sifat ataupun ciri yang menjadi ciri khas dari bangun datar tersebut. Diantara sifat-sifat tersebut ada yang dinakaman dengan simetri. Pada bangun datar terdpat dua jenis simetri yaitu simetri putar dan simetri lipat.
1. Simetri Lipat
Simetri lipat pada bangun datar adalah banyaknya lipatan pada bangun datar yang bisa membagi bangun datar tersebut sehingga setengah bagian dari bangun datar tersebut bisa menutupi setengah bagian yang lain. Garis yang dapat membagi sebuah bangun datar menjadi dua dan kongruen disebut sebagai sumbu simetri. Tidak setiap bangun datar memiliki garis yang dinamakan sebagai sumbu simetri. Ada beberapa bangun datar yang tidak memiliki sumbu simetri sama sekali.
Jika Anda melipat sebuah gambar sehingga gambar itu mempunyai dua bagian yang persis sama, maka gambar tersebut mempunyai semetri lipat dan garis lipatannya disebut garis simetri.
Nama Bangun, Jumlah Simetri Lipat dan Gambarnya :
1). Persegi

Persegi mempunyai 4 simetri lipat, diantaranya meliputi :
- Simetri lipat pertama: A bertemu dengan D dan B bertemu dengan C.
- Simetri lipat kedua: A bertemu dengan B dan C bertemu dengan D.
- Simetri lipat ketiga: A bertemu dengan C BD adalah sumbu simetri yang membagi bangunan menjadi dua bagian yang sama besar.
- Simetri lipat keempat: B bertemu dengan D. AC adalah sumbu simetri yang membagi bangunan menjadi dua bagian yang sama besar.
2). Persegi Panjang
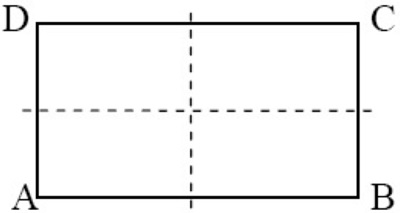
Persegi panjang mempunyai 2 simetri lipat, diantaranya meliputi :
- Simetri lipat pertama: A betemu dengan D dan B bertemu dengan C.
- Simetri lipat kedua: A bertemu dengan B dan D bertemu dengan C.
3) Segitiga Sama Kaki
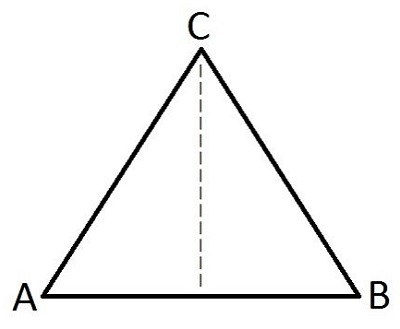
Segitiga sama kaki mempunyai 1 simetri lipat, yaitu :
- A bertemu dengan B, dimana C sebagai sumbu simetri
2. Simetri Putar
Sebuah bangun datar dapat dikatakan memiliki simetri putar apabila ia memiliki sebuah titik pusat dan apabila bangun datar tersebut dapat kita putar kurang dari satu putaran penuh untuk mendapatkan bayangan yang tepat seperti bangun semula. Apabila kita memutar sebuah bangun datar dan hanya bisa mendapatkan bayangan seperti bangun semula dalam 1 putaran penuh, artinya bangun datar tersebut tidak memiliki simetri putar sama sekali.
Berikut ini simetri putar, simetri lipat dan sumbu simetri beberapa bangun datar :
| No. | Nama Bangun Datar | Simetri Lipat | Simetri Putar | Sumbu Simetri |
|---|---|---|---|---|
| 1. | Segitiga samakaki | 1 | – | 1 |
| 2. | Segitiga samasisi | 3 | 3 | 3 |
| 3. | Segitiga sembarang | – | – | – |
| 4. | Persegi Panjang | 2 | 2 | 2 |
| 5. | Persegi | 4 | 4 | 4 |
| 6. | Jajargenjang | – | 2 | – |
| 7. | Trapesium samakaki | 1 | – | 1 |
| 8. | Trapesium siku-siku | – | – | – |
| 9. | Trapesium sembarang | – | – | – |
| 10. | Layang-layang | 1 | – | 1 |
| 11. | Belah ketupat | 2 | 2 | 2 |
| 12. | Lingkaran | tak terhingga | tak terhingga | tak terhingga |
| 13. | Elips/Oval | 2 | 2 | 2 |
Demikian pembahasan secara singkat mengenai Simetri Lipat dan Putar Pada Bangun Datar Beserta Contohnya. Semoga bermanfaat dan berguna bagi kalian. Terimakasih, selamat belajar!